题目链接:https://leetcode.cn/problems/linked-list-cycle-ii/description/
我的思路
第一次遇到这种题,有点被吓到了,不知道什么是链表,被题目里的定义和复杂的描述给唬住了,一直在纠结给出代码中的ListNode类的定义是什么,读懂题意花了很长时间,没有自己的解答思路
纠正
- 理解题意:给的链表其实就是有序的列表,然后这道题里在有序的列表基础上形成了环,那么这种结构就会涉及到几个新的元素:链表起点(叫做头,head)、环的起点(题目里pos给出了环起点的索引),自己一开始感到奇怪,明明给了链表的环起点pos,为什么还要判断是否有环以及求环的起点索引?因为题目里很明确地说了,pos变量不会作为参数进行传递,是评测系统内部的一个参数,表示链表尾链接到链表中的位置,只是为了标识链表的实际情况,因此这只是一个让我们知道这个链表有没有环结构的一个标志,对我们的实际问题求解不会有什么影响和帮助,那么我们要怎么判断这个链表是否存在环呢?
- 题目里也很明确地告诉我们了,只要链表中后续还有节点,就可以一直使用.next指针到达,同时如果这个过程能够一直循环下去的话,就说明链表中存在环(很合理,不然next就是None了)
- 我们要做什么?目标就是找到链表环结构的起点,按照题目的意思来说,也就是链表尾被连接回到了链表中的哪个位置,返回对应的索引值
正确思路
采用快慢双指针的思路,一个慢(速度为1,即1个单位时间走1个节点),一个快(速度为2,即1个单位时间走2个节点)
为什么这么做?因为我们要确定的是环的入口位置,那单纯只靠一个指针来走不太可能能确定这个位置在哪,所以我们要引入两个,且两个指针的速度要不一样,这样他们之间在相同时间内走过的距离会存在一个差值,同时因为环结构的存在,二者会在某一个时刻相遇,那么他们走过的路程、差值、相遇时刻与环的起点位置、环的长度这几个量之间或许存在某种关系,这是我们可以尝试的一个思路。其实或许这个做法在算法题解中是常用的,只是自己第一次接触不太知道,会这么想,后面熟悉后可以举一反三直接用这样的办法,这就是一个“没有为什么”的解法。这种算法叫Floyd判圈算法
Floyd判圈算法用于高效检测序列(如链表)中是否存在环(循环)。其核心解决思路是使用快慢双指针(龟兔赛跑),慢指针每次移动一步,快指针移动两步。如果存在环,两指针必定会相遇;如果快指针到达终点,则无环。此算法能以常数空间复杂度(O(1))和线性时间复杂度(O(n))解决问题,效果极佳。此外,它还能用于寻找环的起点:在两指针相遇后,将其中一个指针重置回起点,然后两指针同速前进,再次相遇点即为环的入口。
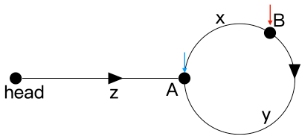
给我们一个如上的链表,我们先假设几个重要的量,从链表头到环起点的距离为z,慢指针刚走到环入口时,快指针已经又走过了环的x个节点,y表示从此时快指针走到环起点还需要走几步,那么环的长度为x+y(注意,这里的“距离”都是包括了起点和终点的,并且指的是有这两段之间有几个节点),慢指针slow速度为1,快指针fast速度为2,我们关键是要找出z为多少
- 首先把快慢指针都放到头部,设为起点,slow = head, fast = head,让他们开始往下走
- 往下走的过程可以用一个while来实现,但在while的开始需要加一个判断语句,如果这个目前元素为空(以fast为例,条件语句为fast == None或者not fast),或者没有下一个元素了(not fast.next),这两种情况都说明这个链表是没有环结构的,自然也不存在所谓的环起点,返回None即可,程序结束
- 如果还能继续往下走,那就继续执行后面的判断,slow每次走1步,所以slow = slow.next,fast每次走2步,所以fast = fast.next.next
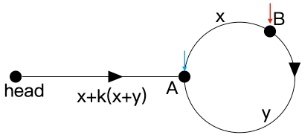
- 我们第一个比较好“拿捏”的地方是slow刚好到了环入口时,即在不断重复3的情况下,当slow刚好要进环时,此时fast可能已经在环中走了k圈,k为正整数,那么fast一共走过的路程为z+x+k(x+y),此时slow走过的总路程为z,因为fast的速度为slow的两倍,所以fast走过的路程也应为slow的两倍,因此有z+x+k(x+y)=2z,计算得出z=x+k(x+y),于是我们就得到了我们想要的关键信息z的一个表达式,因此可以得到:
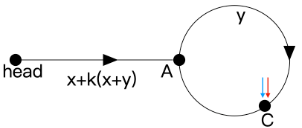
- 让两个指针继续往下走,此时慢指针已经入环了,那么可以肯定在未来某个时刻,慢指针和快指针一定会在环的某个位置相遇,而且我们可以得出,这个位置是在入环后再走y个节点的位置,推导:慢指针刚入环时,快指针距离环入口还需要走y步,那么意味着经过时间y/2,快指针便会回到环入口,此时慢指针走过了y/2*1=y/2个节点,二者继续往下走,当再经过y/2时间时,此时慢指针和快指针刚好都走到了离起点y的位置,如下图所示
- 而我们刚才又得出,链表头离环起点的距离为x+k(x+y),x+y刚好是环长,根据之前的数量关系,上图中C点离环起点还有x步,这不就巧了吗,我们再引入一个新指针ptr,速度也为1,把它先放到链表头,然后同步和慢指针往下走,慢指针此时因为已经入环了,会在环里一直循环下去,当ptr和slow相遇时,这个位置便是我们要求的z(因为z=x+k(x+y),当ptr走过这个距离时,慢指针在环中循环了k圈,并多走了x步,正好回到起点),返回此时的ptr,便是我们要求解的答案
反思
- 读懂题意很重要,不要被一些无关的注释给困住了
- 学会这种思路,下次直接用
结果
48ms (77.26%), 19.31MB (52.66%)