题目链接:https://leetcode.cn/problems/find-first-and-last-position-of-element-in-sorted-array/description/
我的思路
大前提:序列已经按非递减顺序排列好。
题目要求时间复杂度只能为$O(\log n)$,因此不能用简单的指针法(那样的复杂度为n),只能用二分法来求解。用两次二分法,第一次找第一个出现的位置,第二次找最后一个出现的位置,二分法的时间复杂度本身就为$O(\log n)$,用两次加起来$O(\log n)+O(\log n)$也仍然是$O(\log n)$
target出现位置肯定满足条件nums[mid] == target,但也需要进一步判断:
- 第一次出现位置:mid == 0 or nums[mid - 1] < target (有可能回到了列表起点),如果都不符合,那说明nums[mid - 1] = target(这个时候不可能是>target了,否则和先决条件nums[mid] == target以及非递减序列的大前提矛盾),意味着此时的mid还不够靠左,要把mid值往左边移,因此r = mid - 1
- 最后出现位置:mid == len(nums) - 1 or nums[mid + 1] > target (有可能到了列表末尾)
当nums[mid] > target时,应该缩短右侧区间,即r = mid - 1,继续做判断,当nums[mid] < target时,应该缩短左侧区间,l = mid + 1
思路很明确,但是在执行的时候,还是卡在了如何更新l和r上,要么是选取不合理返不回正确的结果,要么是取值不当让程序陷入死循环
纠正
始终记住:mid永远在l和r的中间,l和r才是边界。区间的变化无非两种情况,可以通过判断mid值的移动趋势来执行操作,这也是二分法的核心所在:
要把mid值往左移动,意味着要从右边缩小区间,因此应该改右边界r = mid - 1(如果把此时的l移动到mid或者mid-1,无论怎样都相当于把l给扩大了或者不变,扩大的情况会让mid值更大,不满足题意,不变的话就会让程序陷入死循环)
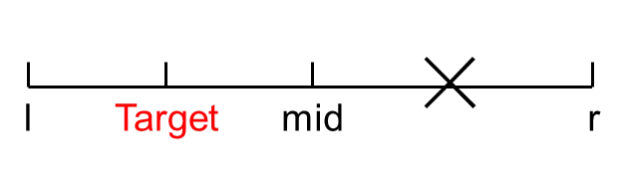
- 在这道题里,nums[mid] > target,说明区间“往右伸”得太多了,因此肯定要从右边开始缩减,此时mid和mid之后范围的数值都没有用了,因此除开这些没用的数值,r = mid - 1,这就是-1的由来,如下图所示(注意,这里的坐标轴指的是索引,不是代表序列中的数值,target表示的是target所在的位置)
要把mid值往右移动,说明要从左边缩小区间,因此应该改左边界l = mid + 1(如果把此时的r移动到mid或者mid+1,那就相当于把r给缩小了,会让mid值更往左靠,不满足题意)
- 同样地,nums[mid] < target,说明区间“往左伸”得太多了,因此肯定要从左边开始缩减,此时mid和mid之前范围的数值都没有用了,因此除开这些没用的数值,l = mid + 1,这就是+1的由来
反思
- 一定要仔细仔细读题,充分利用好题目中的所给条件,并读懂题意,看懂要求,已经好几次没有好好利用题目里给的“非递减序列的条件了序列”的条件了
- 要学习算法复杂度的表示方法,不然在有的题目里会有限制,看不懂
- 培养抽象思维,将问题进行抽象表达,找到共性的特点
- 可以让代码尽可能简单一些(当然,这是进阶要求,现阶段对自己的要求还是能顺利通过解答即可),这道题里一开始的思路是要判断两次,那会很容易想到写两个子函数,但其实这两个子函数有很大篇幅的share部分,统统单独写出来就会篇幅很长不够简洁,完全可以写到一个函数里面
结果
0ms 100%, 18.74MB 54.33%