题目链接:https://leetcode.cn/problems/kth-largest-element-in-an-array/description/
我的思路
又是一道中等题目的题,并且今天也是才学排序算法,因此拿到这题还是有点发怵,除了最基本的用排序方法外没有什么别的思路,但这样的时间复杂度不符合题意,所以还是要想别的办法。
题解:快速选择法
核心包括两部分,哨兵划分和递归
- 哨兵:随机取数组中的一个数作为基准数(最左、最右或者随机取),之后遍历剩下的元素,把小于基准数的放到哨兵的左边,大于的放到哨兵的右边
- 递归:继续对左子数组和右子数组执行哨兵划分,直到子数组的长度为1时终止
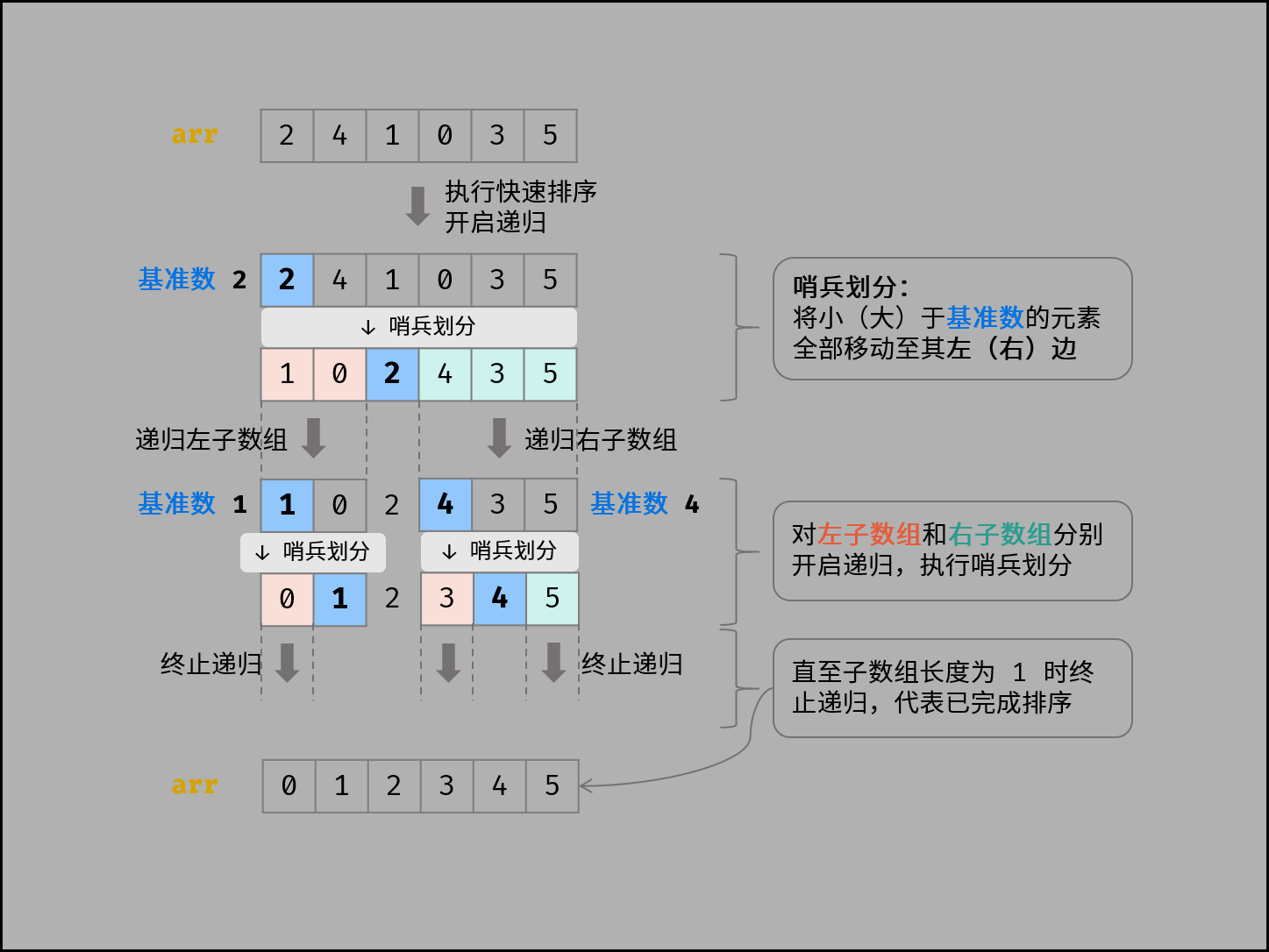
以上过程可以用题解的图来很好解释:
放到算法层面,我们可以定义三个列表来实现上述操作:small, equal和big,把和pivot相等的值放进equal,更小的放进small,更大的放进big,这样一来我们就得到了这个数组中前len(big)大的数字,执行完放数字操作后比较len(big)和k的大小:
- 如果len(big) < k,说明我们的pivot选得刚好(我们想要的值全都在equal里)或者选大了(我们想要的值在small里)
- 如果len(big) = k,说明我们的pivot选得刚好(有可能第k个最大的值在原数组中有重复,equal和big有交集)或者刚好选小了(第k-1个最大的值在equal中),这种情况下第k个最大的值包含在了big中
- 如果len(big) > k,说明我们的pivot刚好选小了(第k个最大的值有重复的情况下,全部包括在了big中,euqal中是第k-1个最大的值)或选小了,这种情况下第k个最大的值也是包含在了big中
针对第2、3种情况,很好对其进行抽象,只要k ≤ len(big),那我们只要再对big这个子数组进行一次快速选择即可,最后一定能找到我们想要的那个值
但对于情况1,需要一些巧思处理,这时关键是确定:第k大到底是不是pivot(在equal中),还是在small中,(以下讨论仅限于len(big) < k的情况),在这种情况下:
- 如果
k ≤ len(big) + len(equal),说明第 k 大的数就是 pivot,因为它必然落在 equal 中,直接返回 pivot 即可。 - 如果
k > len(big) + len(equal),说明第 k 大的数在 small 中。此时我们递归在 small 中继续查找,同时需要将 k 更新为k - len(big) - len(equal),因为针对原数组来说,前len(big) + len(equal)大的数字已经包含在了子数组big和equal中(这里可能会陷入一个思维陷阱:就算有重复的元素,那它也并不会影响我们的最终判断,比如1,2,2,2,3,第3大的元素仍然是2),所以我们这里可以直接排除掉len(big) + len(equal)这部分的元素,在子数组small中找第k - len(big) - len(equal)大的元素,就是相较于原题目而言我们要的答案
所以情况1的判断条件可以抽象为 k 是否 >len(nums)-len(small) = len(big) + len(equal) ,如果满足,那就再对small这个子数组做 k - len(big) - len(equal) 的快速选择即可
其实本题还有另一种思路,也是同样只将注意力放到数组中“更大”的那部分元素即可,但这种思路执行起来遇到了OOM/OOT的问题,在一个特别长的测试案例上(长度可能上万)卡住,内存占用/耗时超出限制,这种思路是:
- 定义一个quick_start函数,输入为(nums, l, r, k)
- 随机选取一个pivot,定义store_index初始化为l
- 遍历数组,如果nums[i] ≥ pivot,就将nums[store_index]和nums[i]对调,同时将store_index加1,比如[3,2,1,5,6,4],假设pivot取4,3,2,1都不大于4,直到5>4,此时store_index仍为0,因此将nums[0]处的3和5对调,变成[5,2,1,3,6,4],store_index变为1,接着6仍大于4,再将nums[1]处的2和6对调,变成[5,6,1,3,2,4],store_index变为2,最后2不大于4,不执行操作
遍历完毕后,store_index为2,将nums[2]处的1和pivot进行对调,得到[5,6,4,3,2,1],这样一来,就以store_index为分界,nums[:store_index+1]是原数组中前store_index + 1大的数字的集合,因此只要判断store_index和k的大小即可
- 如果store_index + 1 = k,说明pivot刚好,返回pivot
- 如果store_index + 1 < k,说明pivot取大了,继续对nums[store_index:]的元素以前k - store_index为目标进行快速选择
- 如果store_index + 1 > k,说明pivot取小了,继续对nums[:store_index]的元素以前k为目标再进行快速选择
判断条件和第一种思路基本一致。其实这两种思路本质上都是一样的,划分子区间,然后看子区间的长度,只是执行起来用了不同的方法,第一种思路是把大的数组分割到了几个子数组中,这样能够很大程度上减少内存开销,接着再比较k和子数组长度的关系,做进一步的判断,第二种思路则是比较store_index和k的大小关系,本质上也是在划分子数组,只是这里没有另外单独生成子数组,而是始终在原数组上进行操作,看似减小了内存开销,但增加了时间成本。提交结果方面,只有第一种思路的代码顺利通过了测试,但是第二种理论上也是正确的。
反思
- 充分利用好“分治”(devide & conquer)的思想,用好哨兵pivot
- 因为我们要找的是第K大的数字,因此我们只需要关注更大的那一部分数字,那怎么得到更大的那部分数字呢?就是用哨兵来进行区分,接着再根据我们选出来的这部分数字有几个,以及我们要判断的k值作比较,动态调整
- 为了提升算法的稳定性,哨兵基准数通常采用随机的方式进行选取(统计学上可证明这样做能将总的时间期望降到最低)
结果
35ms 94.45%, 29.23MB 21.33%