题目链接:https://leetcode.cn/problems/n-queens/description/
思路
依旧是回溯法,深度优先搜索,dfs,从第一行的第一列第一个元素出发,把所有横向纵向的可能性都判断一遍,在遍历的过程中加入判断条件进行剪枝。仔细阅读一下这道题,可以把限制条件抽象为以下两点,并通过对应的方法来进行判断:
- 同列不能有两个元素,定义一个col列表,长度为n,表示每次遍历中每一列的元素占有情况,如果某一列上放了queen,就将对应位置更改为True,这个变量在每次循环中需要回溯
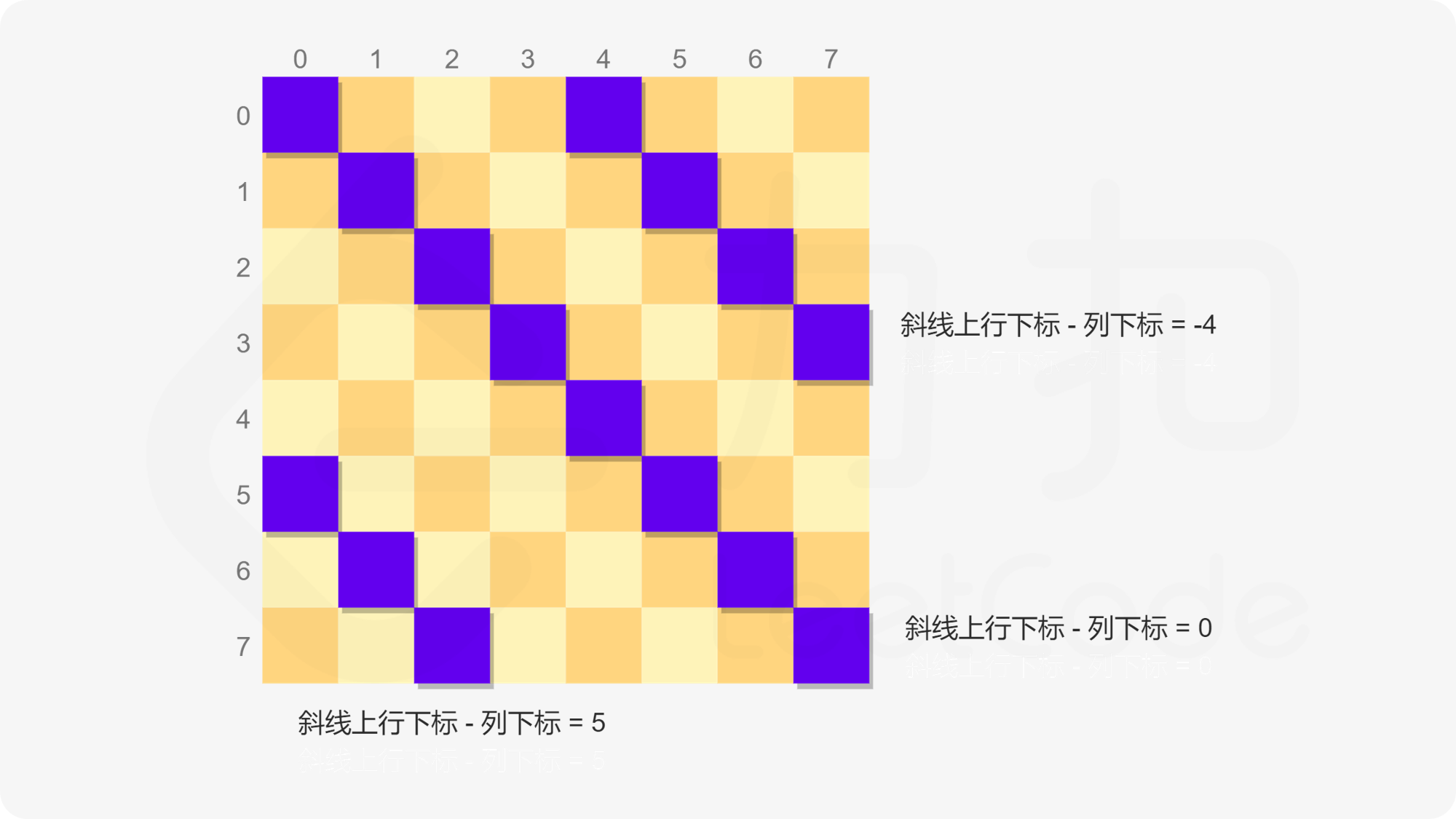
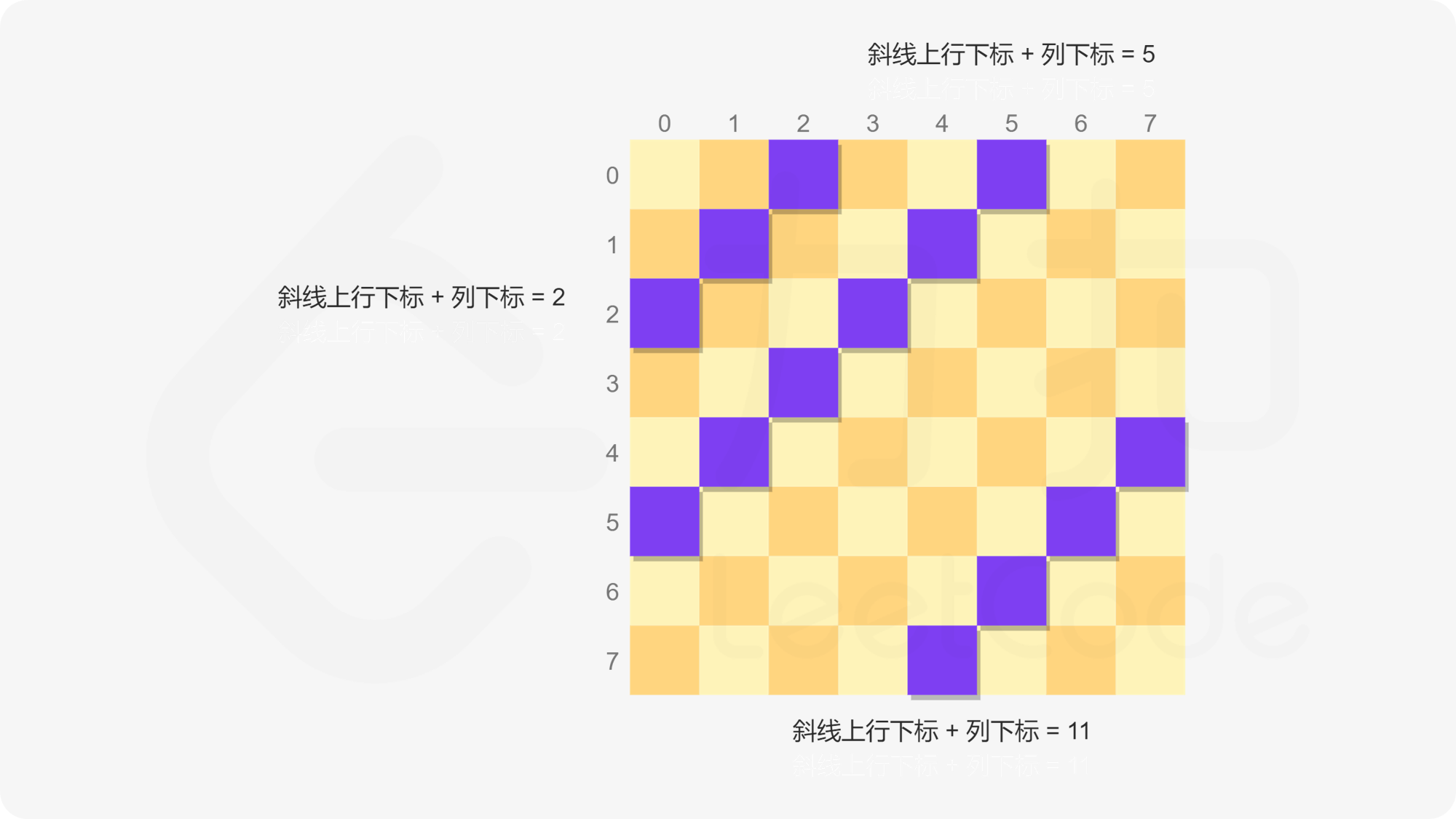
- 对角线上不能有两个元素,通常而言,对角线上的元素比较特殊,满足某种数学关系,我们可以抓住这个数学关系来进行判断,在↘方向上的对角线元素满足$i - j$始终为固定值,在↗方向上的对角线元素始终满足$i + j$为固定值,如下图所示
也就意味着,比如当前在$[2, 3]$位置处放了queen,那么对于其他任意满足$i+j=2+3 =5$以及$i-j=-1$的位置都不能再放queen了。于是乎,我们可以定义两个对角元素的考察列表ldiag和rdiag,因为n是固定的,有$0\leq i + j\leq n-1+n-1=2n-2$,$0-(n-1)=-n+1\leq i-j\leq n-1$,那么两个考察列表的长度分别为$2n-2+1=2n-1$以及$n-1-(-n+1)+1=2n-1$,是相同的,这样一来就能把所有可能的情况涵盖进去(这里尽管$i - j$可能会是负数,但是我们只要定义了足够长的列表,当索引为负值时,从逆向取值,也是能够满足我们的要求的,我们在这里只是要判断某个$i - j$是否已经被占用了),如果在某个位置$[i, j]$放了queen,那么就分别将ldiag$[i + j]$以及rdiag$[i - j]$的位置设置为True即可,这两个变量也是需要回溯的
- 于是乎,根据上面的讨论,我们就得到了以下dfs函数中的核心部分:
for j, ok in enumerate(col): #需要考察col的情况
if not ok and not ldiag[i+j] and rdiag[i+j]:
queen[i] = j #记录下在第i列中,queen被放到了第几行中,这个变量不需要回溯,因为如果前一个不满足的话,后面会直接覆盖掉前一个值,直到找到合适的解
col[j] = ldiag[i + j] = rdiag[i - j] = True
backtrack(i + 1) #递归下一列
col[j] = ldiag[i + j] = rdiag[i - j] = False #回溯,防止污染下一次判断- dfs函数传入的变量为i,表示当前考察的是第几列
以上整个递归过程可以用下面的递归树来表示,红色实线箭头表示递归,虚线表示回溯,由于判断条件的存在,不会递归到底,而是会在树内进行剪枝,提高运行效率:
反思
- 不能加上“在一行只尝试放一个皇后的位置”的判断条件以试图减少判断次数来优化算法,因为这样可能会漏掉可能的解,在n比较大的时候,可能在一行会有若干个符合条件的位置,因此不能在找到一个答案后就不遍历后面的位置了,会出错
- 以后可以用递归树的形式来帮助自己理清思路,弄清楚有几个节点、题目是什么意思
结果
时间复杂度:$O(N!)$
空间复杂度:$O(N)$
已是最优解