题目链接:https://leetcode.cn/problems/valid-triangle-number/description/
我的思路
这题是很典型的初中数学题,根据三条边的大小来判断是否能组成一个三角形,想到判断条件为:两边之和大于第三边,两边之差小于第三边。很容易想到暴力枚举法,但这样的效率很低,因此联想到用双指针法,但也没有做进一步的思考,就直接开始动手了
纠正
首先将nums排序,从中取出已经排好序的三个数$a\leq b\leq c$,那么根据判断条件,要让这三条边能构成一个三角形,有:$a+b>c,a+c>b,b+c>a$,因为已经排好序了,那么后面两个条件必然成立,因此我们的目标转换为判断$a+b$是否大于$c$
这里有一个很容易困惑的点,就是第二个条件“两边之差小于第三边”是否能满足?根据上面的讨论,$a+c>b$和$b+c>a$是必然成立的,那么根据这两个式子可以推出:$|b-a|=a-b<c,|b-c|=c-b<a,|a-c|=c-a<b$也必然成立(分别将两个变量移到不等号右边),那么第二个条件天然地满足了,只剩下要判断两个短边的和是否大于长边
因此我们可以固定长边,取$c=\mathrm {nums}[i],\forall i\in [2, n-1]$,接着在$[0,i-1]$中进行双指针判断,初始化$l=0,r=i-1$,如果$\mathrm{nums}[l]+\mathrm{nums}[r]>\mathrm {nums}[i]$,就说明从$l$到$r$之间的每个数都满足这个条件,能够构成三角形(因为已经事先排好序),就可以让$ans$加上$r-l$
优化
这题还有一个更巧妙的操作,但理解起来比较困难,就是用卷积+快速傅里叶变换,numpy包包含了快速傅里叶算法,能有效降低时间复杂度(因为这道题中数组中数字范围小于1000,比较小,因此这个方案可行)。计算不符合条件的情况数(两边之和小于第三边),然后再用一共有几种情况$C_{nums.size}^3$减掉不合理的情况数,就能够得到最终答案,为什么要这样做,通过下面的讨论可以找到答案
这里用到了两个关键定理:
- 卷积定理:频域相乘等价于时域卷积,时域卷积等价于频域相乘,即$\mathcal{F}\{f*g\}=\mathcal{F}\{f\}\cdot\mathcal{F}\{g\},\mathcal{F}\{f\cdot g\}=\mathcal{F}\{f\}*\mathcal{F}\{g\}$
- 时域卷积的定义:$(f∗g)[k]=\sum_if[i]⋅g[k−i]$,对于每一个可能的和$k$,把所有能组成$i+j=k$的组合的乘积$f[i]g[j]$累加,换句话说可以写成:$(f*f)[s]=\sum_{x+y=s}f[x]f[y]$,表示两数相加和为$s$的组合次数
首先构建频率数组,$cnt[x]$表示$x$在所给数组中的出现频次,接着结合快速傅里叶变换做自卷积,得到$cnt2[s]$,表示两边之和为$s$的组合数(可能有几种情况)。参照上面的类似思路,我们固定$cnt$,取其中的元素所对应的边长作为最长边来考虑(考虑的背景是,根据三角形组成判断条件,
对每个三元组,最大边必须小于另外两边之和),那么我只需要考察$cnt2[:cnt.size]$这部分的元素,后面的部分没有合理的最长边来与之对应了,因此不在考虑范围内
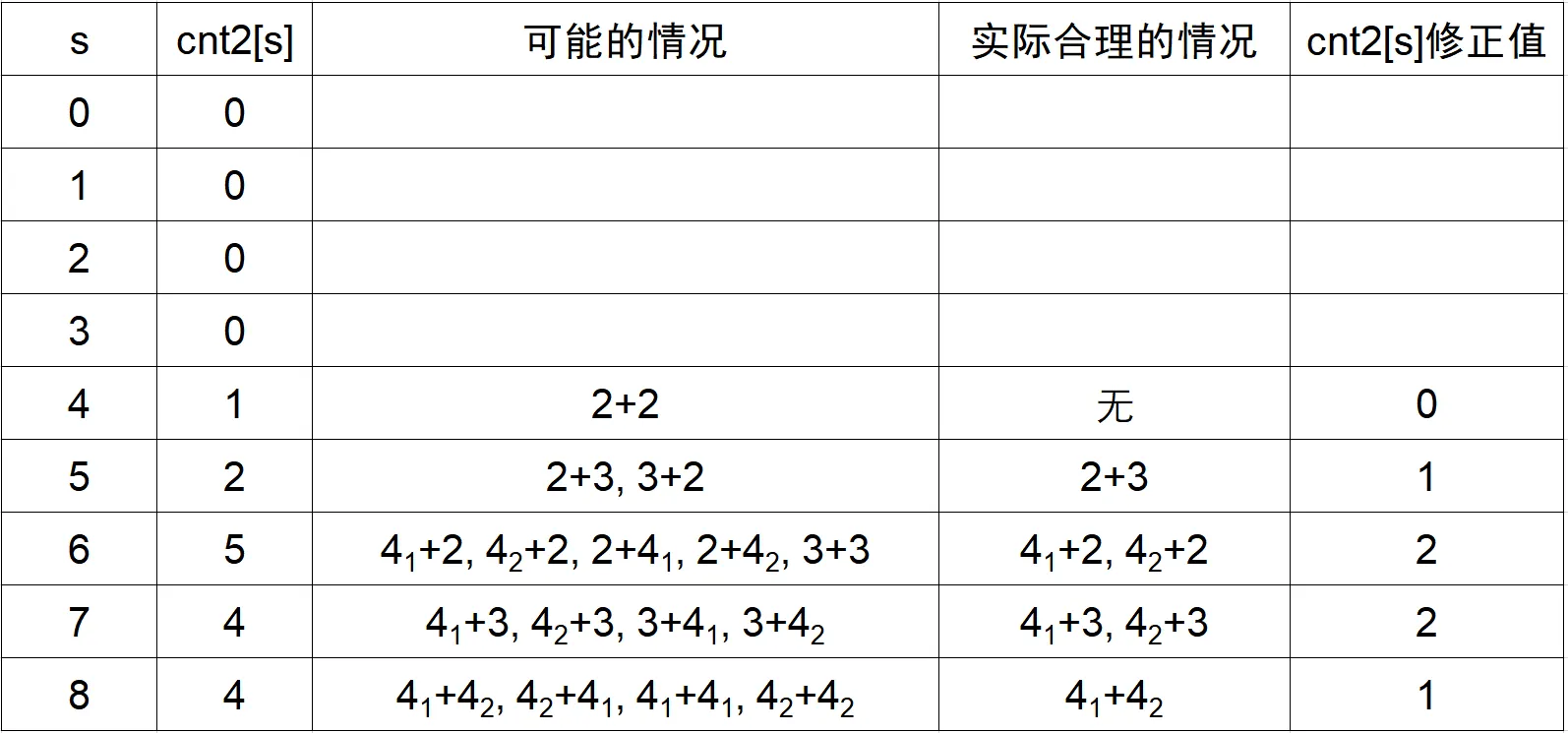
需要注意的是,卷积过程中会出现两种情况:(1)自己加自己;(2)顺序调换相加得到相同结果,这两种情况都会算入到计数中,如下表所示:
因此我们需要对$cnt2$中的值进行修正,考虑上面说到的两种情况:
- 自己加自己,相当于把自己*2,因此得到的数一定为偶数,这种情况只会出现在$cnt2$的偶数索引处,因此只需要将$cnt2$偶数位置处的值减掉原来的值$cnt$即可(比如这里$cnt[4]=2$,意味着原来数组中有2个4,$cnt2[8]$中会包含2个自相加的结果,在这道题中我们不能重复利用元素,因此需要减掉2),写成表达式就是:$cnt2[::2]=cnt2[::2]-cnt[:]$,但因为我们上一步中对$cnt2$进行了截取,只取了$cnt.size$这一部分,在取偶数索引部分时,其实只对应了$cnt$的$(cnt.size+1)//2$部分,因此在代码实现时,需要写成$cnt2[::2]-=cnt[:(cnt.size+1)//2]$(以上表为例,$cnt2$被截取$[0:4]$这部分,取偶数索引,对应0,2,4,只有三个元素,这几个元素才会包含自相加的情况,我们为了修正,需要减掉其对应原始数组中元素的出现频次,即0,1,2这三个元素的频次,而在$cnt$中,这三个元素对应前$5+1//2=3$个元素,因此需要这么计算)
- 顺序调换得到相同结果,这种情况比较好处理,在完成第一种情况的处理后,再将$cnt2$整体整除2即可,就能得到修正值
这样一来,我们便得到了截取和修正后的$cnt2$数组,接着固定长边进行不合理情况的计算。对于$cnt[i]$,$\mathrm{sum}(cnt2[:i])$表示了两边和小于等于$cnt[i]$的情况总数,我们可以用一个$\mathrm{cumsum}$函数来计算累计求和,实现上面的步骤,得到$pre2=\mathrm{cumsum}(cnt2)$,若某个边长在数组中出现多次,其不合理情况也应按出现次数重复计算,因此还需要将$pre2*cnt$,得到每个长边所对应的不合理的情况总数,最后我们将视角放回到全局,计算出总的不合理情况数$\mathrm{sum}(pre2*cnt)$,再用$C_{nums.size}^3$减掉这个数,即可得到最终结果$C_{nums.size}^3-\mathrm{sum}(pre2*cnt)$
反思
- 在FFT法中:因为我们算出的$cnt$是“计数数组”,表示每个元素的出现频次,因此其长度天然地等于$\max (nums)+1$,其末尾元素对应的索引就表示了原始数组中的最大值,通过自卷积操作,算出了任意两边和的情况计数数组$cnt2$,对应的长度天然地等于$2*cnt.size+1$,其末尾元素对应了原始数组中的最大值*2
- 对于这类题我们要找到一个固定约束,比如这道题中固定最长边,再考虑其他边的情况,这样才能不失一般性,不然会很容易重复计算/漏掉情况
结果
时间复杂度:$O(N+m\log m), m=\max(nums)$
空间复杂度:$O(N)$
已是最优解