Data link layer is responsible for delivering data from one node to another node, which means that the duty scope of data link layer is only node-to-node. A packet at the data link layer is called a frame. Any mistakes made in physical layer is supposed to be solved in data link layer.
Types of data link layer:
- Point to point link: it consists of a single sender at one end of the link and a single receiver at the other end.
- Broadcast link: it can have multiple sending and receiving nodes all connected to the same, single, shared broadcast channel. If one node transmits a frame, a copy of it will be received by all the other nodes. To avoid multiple access problems, coordination mechanism should take into consideration. A case in point is mobile phone communication.
Components of data-link layer
To better understand the functionality and services of data-link layer, it can be divided into two sublayers: data-link control (DLC) sublayer and media access control (MAC) sublayer.
For P2P link, MAC sublayer is empty, as it is designed to deal with issues specific to broadcast link like multiple access problems.
Services provided by data-link layer
Framing: from bits from the physical layer to datagram (packet, frame). A frame consists of a data field, in which the network layer datagram is inserted and a number of header fields.
Flow control: prevent the sending node from overwhelming the receiving node
Medium access: MAC protocols in the data-link layer specify the rules by which frames are transmitted onto the link. They serve to coordinate the frame transmissions of multiple nodes.
Error detection: each node in the network must equip with the capability to detect the presence of one or more errors. It is achieved by setting error detection bits in the frame in sending node and performing an error check at the receiving node.
Error correction: not only detect, but also correct them.
Reliable delivery: to guarantee to move each network layer datagram across the link without error
Half-duplex or full-duplex: determine a node could transmit and receive simultaneously or not (半双工,双工)
Framing
At the sending node, the data-link layer encapsulates each datagram into a frame and then passes it to the physical layer whose job is to move the individual bits within the frame from one node to the next in the form of signals. Physical layer only contains bits, which has no structure. It converts bits into signals to be transmitted.
While at the receiving node, the data-link layer is responsible for packing bits into frames so that each frame can be distinguished from the others.
Byte-oriented framing
- Definition: each frame starts and ends with a specific byte, often the same byte, called a flag byte.
- Problem: the character used for the flag could also be a part of the data. To solve this, the sender's data-link layer inserts a special escape byte (ESC) just before each accidental flag byte in the data. (在传输的数据比特流中包含的flag比特前插入一段ESC比特,告诉数据层继续找下一个flag,防止误检) An escape byte means throwing it away.
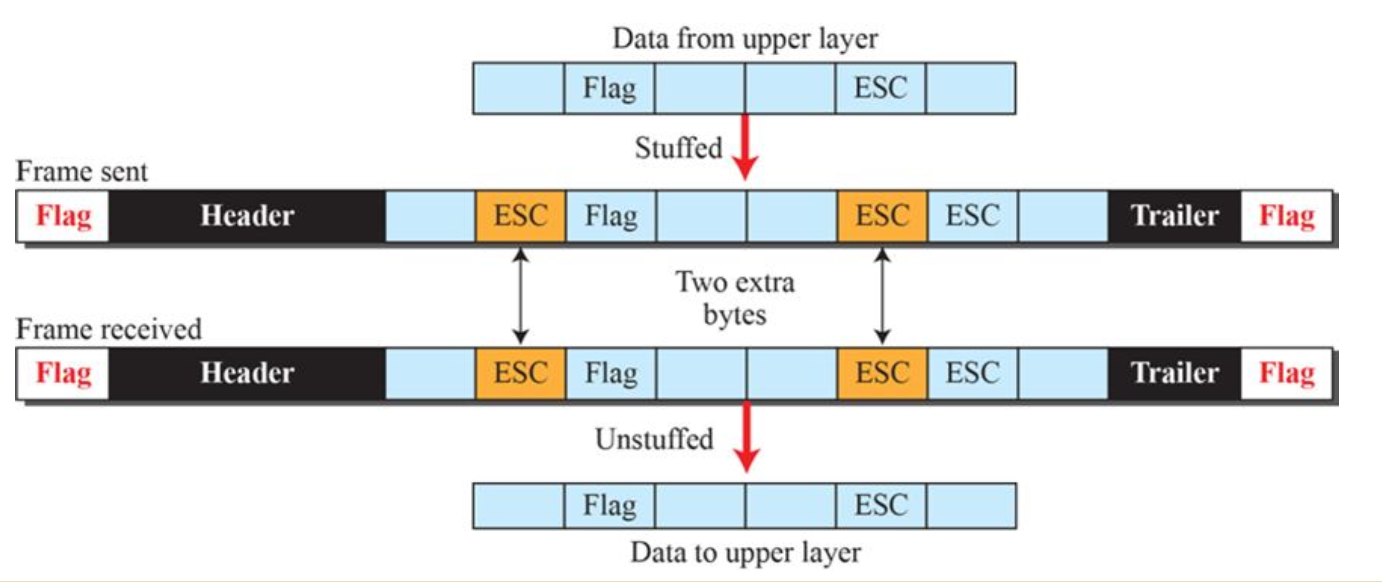
- Application: it is usually used in point-to-point protocol (PPP)
Bit-oriented framing
- Definition: each frame starts and ends with a special 8-bit pattern flag.
- Problem: similar to the byte-oriented framing, the flag pattern can also appear in the data. To solve this, we can stuff a single bit to prevent data pattern from looking like a flag (bit stuffing). Whenever the sender's data-link layer encounters a 0 bit and five consecutive 1 bits in the data, it adds an extra 0 bit. (Regardless of the value of the next bit) It guarantees that the flag field sequence does not inadvertently appear in the frame.
- Application: it is used in high-level data-link control (HDLC) protocol. Bit stuffing also enables more transitions in the signal which help the physical layer maintain synchronization.
Error detection and correction
To be able to detect or correct the errors occurred during data transmission, we need to send more extra bits along with our data.
Two basic strategies to deal with bit errors:
- include only enough redundancy in the data to allow the receiver to deduce that an error has occurred (but unaware of which error happens) and have it request a retransmission (error detection)
- include enough redundant information in the data to enable the receiver to deduce what the transmitted data must have been (error correction)
Parity check 奇偶校验
Single parity bit
Problem: if two or any even number of bit errors occur in a single-bit parity scheme, it will result in an undetected error
Two-dimensional parity
Single bit error can be both detected and corrected (by flipping the number). But for two or more bits error, it can only be detect and cannot be corrected.
Example:
Sent data: (no error)
$$ \begin{array}{ccccc|c} 1 & 0 & 1 & 0 & 1 & 1 \\ 1 & 1 & 1 & 1 & 0 & 0 \\ 0 & 1 & 1 & 1 & 0 & 1 \\ \hline 0 & 0 & 1 & 0 & 1 & 0 \\ \end{array} $$
Correctable single-bit error: (it can be detected that row 2 and column 2 has an error)
$$ \begin{array}{ccccc|c} 1 & 0 & 1 & 0 & 1 & 1 \\ 1 & \mathbf 0 & 1 & 1 & 0 & 0 \\ 0 & 1 & 1 & 1 & 0 & 1 \\ \hline 0 & 0 & 1 & 0 & 1 & 0 \\ \end{array} $$
However, two bits error can be detected but it's hard to distinguish where the error exactly is, hence it's difficult to be corrected:
$$ \begin{array}{ccccc|c} 1 & 0 & 1 & 0 & 1 & 1 \\ 1 & \mathbf 0 & 1 & 1 & 0 & 0 \\ 0 & 1 & \mathbf 0 & 1 & 0 & 1 \\ \hline 0 & 0 & 1 & 0 & 1 & 0 \\ \end{array} $$
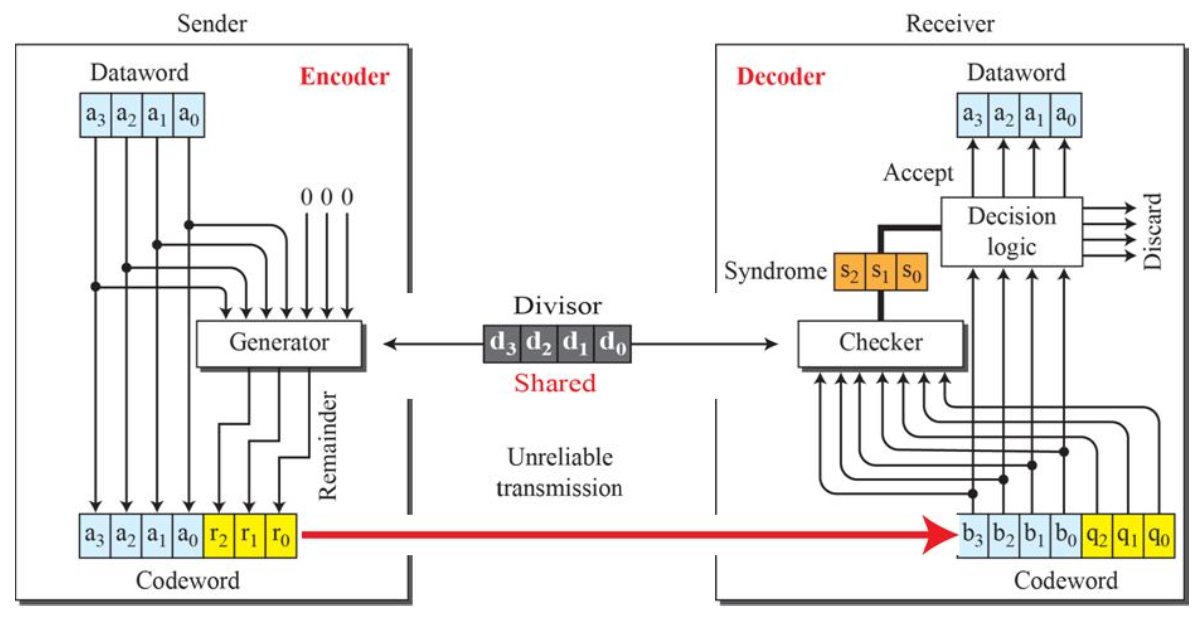
Cyclic redundancy check (CRC) 循环冗余校验
Suppose the sending node wants to send a data word of size $d$ bits. The sender and receiver must agree in advance on an $n+1$ bit pattern, known as a divisor. At the transmitter, the size of the data word is augmented by adding $n$ 0s to the right-hand side of the word. The $d+n$ bit result is fed into a generator which divides (i.e., modulo-2 division) the augmented data word by the divisor. The quotient of the division is discarded while the remainder (of size $n$ bits) is appended to the data word to obtain a code word (of size $d+n$ bits).
At the receiver, the code word (probably corrupted during transmission) is fed into a checker, which is a replica of the generator and divides the received code word by the divisor. The remainder of the division is called a syndrome (of size $n$ bits)
- Application: it is widely used in computer networks (LANs and WANs)
CRC codes are also known as polynomial codes. International standards have been defined for the divisors (used in the generators and checkers). Each of the CRC standards can detect burst errors of $n$ bits or fewer.
Flow control
It is realized by establishing a feedback mechanism between the receiving and sending nodes. The data-link layer at the sending node tries to push frames towards the data-link layer at the receiving node.
Error control
Data-link layer must offer error control services to ensure that the data is delivered with the desired level of reliability.
It is responsible for:
- Detect and discard the corrupted frames
- Keep track of lost and discarded frames and resend them
- Recognize the duplicate frames and discard them
- Buffer the out-of-oder frames until the missing ones arrive
It requires the use of sequence numbers for frames and acknowledgement numbers of the acknowledgements (ACKs).
Automatic repeat request (ARQ) protocols
Stop-and-wait protocol
In this protocol, a sender sends one frame at a time and then waits for an ACK before sending the next one. Thus, there can be only one frame or ACK in the channel at any time. This protocol is proposed to ensure the reliability of data transmission.
Both the sender and receiver use a sliding window (an imagery box) of size 1, $S$ is the sequence number of the sent frame in send window while $R$ is the sequence number of the next frame expected in receive window.
Features:
- Each data frame header carries a CRC, allowing the receiver to compute syndrome for each received frame and detects and error if all syndrome bits are not 0 bits. The corrupted frame is then silently discarded. This silence of the receiver is a signal for the sender that the frame was either corrupted or lost.
Efficiency of SAW protocol with error:
- Let $P$ equals to the probability of an error in the transmission of a frame or in ints ACK.
- $T_{out}$ = time-out interval = $D_{total}$
- $X$ = amount of time it takes to transmit a frame and receives its ACK. This time accounts for retransmissions due to errors.
Thus, $1-P$ is the probability of successful transmission.
The average number of transmissions that need to be done until (and including) first correct arrives is:
$$\frac 1 {1-P} $$
Then, the average number of failed transmission before (and excluding) first correct arrives can be derived as:
$$\frac 1 {1-P} -1 = \frac P {1-P} $$
Bandwidth-delay product: determines the number of bits needed to fill up the whole channel. To use the maximize capacity of channel, a sender should transmit a burst of data whose size is twice of the bandwidth-delay product. Thus, there can be 2 $\times$ bandwidth $\times$ delay bits in transmission at any time.
Go-Back-N protocol
In this protocol, a sender can transmit several frames before receiving ACKs, but a receiver can only buffer one frame. In that case, there can be several frames and ACKs in the channel at the same time.
The sequence numbers in Go-Back-N protocol are modulo $2^m$. An acknowledgement number in this protocol is cumulative and defines the sequence number of the next frame expected. For example, 7 indicates that all frames with sequence numbers up to 6 have arrived safely and the receiver is now expecting a frame with sequence number 7.
Window
Send window is an imaginary box covering the sequence numbers of data frames which are either in transit or can be sent. The maximum allowable size for the send window is $2^m-1$. Three variables ($S_f, S_n, S_{size}$) are used to define the size and location of send window at any time.
- $S_f$: number of outstanding frames, which are sent but not acknowledged
- $S_n$: number of frames that can be sent when accepted from upper layer
- $S_{size}$: send window size, whose maximum number is $2^m-1$
In this protocol, the size of the receive window is always 1. $R_n$ defines the sequence number of the next frame expected.
Efficiency of Go-Back-N protocol
Transmitting $N$ frames costs time $Nd_{trans}$. Let $D_{tot}$ be the total time between the transmission of a frame and reception of its ACK. $Nd_{trans}\geq D_{tot}$. If $Nd_{trans} = D_{tot}$, which means that there is no error cases and no time is wasted for transmission, the efficiency can be $\eta_0=\frac{Nd_{trans}}{D_{tot}}=1$. Otherwise, if $Nd_{trans}<D_{tot}$, the efficiency will be $\eta_0=\frac{Nd_{trans}}{D_{tot}}<1$.
Scenarios with errors:
Average number of failed transmission before (and excluding) a correct arrival is $\frac P {1-P}$. When an error occurs, the entire window of $N$ frames must be retransmitted. Thus, the average number of frames transmitted until (and including) a correct arrival is $E[X]=1+\frac P {1-P}N$. Therefore, the efficiency with errors can be expressed as: $\frac 1 {E[X]}=\frac 1 {1+\frac P {1-P}N}$.
Selective-Repeat (SR) protocol
In SR protocol, only selective frames, i.e., the ones which are actually lost, are resent.
Window
Three variables ($S_f, S_n, S_{size}$) are used to define the size and location of send window at any time (as in the case of Go-Back-N protocol).
However, the maximum allowable size for the send window in SR protocol is $2^{m-1}$, which is much smaller than the Go-Back-N protocol. Meanwhile, the receive window is the same as the size of the send window.
Optimal frame size considering pipelining
Assume that the message has $L$ bits. Then it is separated into frames ($K$ bits per frame). Let $H$ be the length of header, then each frame will have a length of $H+K$ bits. If the data rate is $R$, $d_{trans}$ will be $\frac{H+K} R$.
There are altogether $\frac L K$ frames. Thus, the total transmission time over $M$ links is expressed as:
$$D_{tot} = \left [\frac L K +(M-1)\right ]\left(\frac{K+H} R\right)=\frac L K\left(\frac{K+H} R\right) + (M-1)\left(\frac{K+H} R\right) $$
The first part is called transmission delay, the second one is pipelining delay. Small frames will reduce the pipelining delay but increase the transmission delay due to additional headers. However, large frames reduce header overhead but increase the pipelining delay. Ignoring that $K$ must be an integer, setting $\frac {dD_{tot}}{dK}$, we get:
$$K_{opt} = \sqrt{\frac {LH} {M-1}} $$